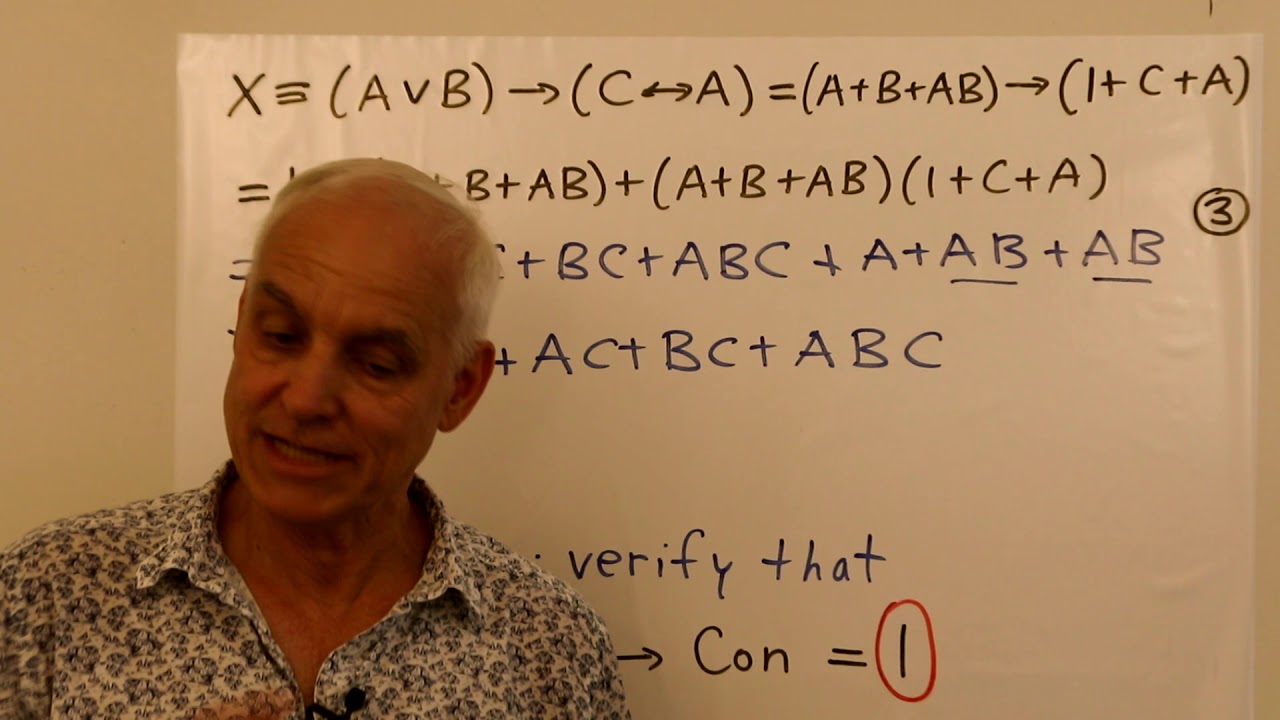In this video we explain how the Algebra of Boole allows a systematic framework for evaluating logical deductions in Propositional Logic (PL). We are following the unique insights of George Boole, to achieve what has been a prime objective in philosophy since the time of Aristotle and the Stoics, and which was at least roughly envisioned by Leibniz. Given a logical argument involving several premises formulated with the usual logical connectives of PL and a desired conclusion, we give a two step method for deciding whether or not the argument is valid. First there is a reduction or simplification of all the ingredients as Boole polynumbers. Then there is the simplification of the statement which encodes the product of the premises implying the conclusion. This approach is particularly suited for computer application, especially when polynomial algebra routines have been augmented with Boole reduction.
0 Comments